Sumber Gambar:pixabay.com
Postingan kali ini akan membahas mengenai Fungsi, Komposisi Fungsi, dan Invers Fungsi di matematika, bagi kalian yang belum mempelajarinya atau sudah mempelajarinya tetapi sudah lupa, nah postingan ini sangat cocok untuk kalian baca dan pelajari, oke langsung saja ke materinya.
A.pengertian Fungsi
Fungsi adalah pemetaan dari setiap anggota dimana menghubungkan setiap anggota A dalam suatu himpunan yang dinamakan domain(daerah asal) kepada anggota himpunan lain dengan tepat satu anggota himpunan B atau juga dengan suatu nilai tunggal f(x) dari himpunan yang kedua yang di sebut kodomain(daerah kawan),kemudian himpunan nilai dari hasil tersebut disebut dengan range (daerah hasil).
Keterangan:
- Himpunan A adalah domain (daerah asal)
- Himpunan B adalah kodomain (daerah kawan)
- Himpunan anggota B yaitu C (f(x)) adalah range (hasil)
Sifat-sifat Fungsi :
1).Fungsi Injektif(satu-satu)
Dimana fungsi injektif(satu-satu),hanya mempunyai satu kawan saja,misalnya fungsi
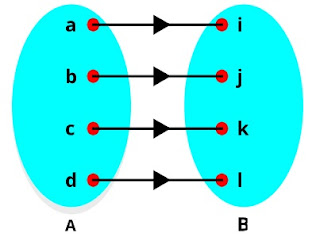
f menyatakan A ke B atau f:A→B,dimana setiap anggota di dalam B hanya memiliki satu kawan saja di A,sehingga fungsi injektif apabila a ≠ b berakibat f(a) ≠ f(b) atau ekuivalen, jika f(a) = f(b) maka akibatnya a = b,untuk contohnya bisa di lihat gambar di bawah ini:
2).Fungsi Surjektif
fungsi surjektif dimana setiap elemen himpunan B yaitu merupakan bayangan dari satu atau lebih elemen himpunan A,atau pada fungsi f:A→B,dimana setiap b∈B mempunyai kawan di A.
3).Fungsi Bijektif (Korespondensi satu-satu)
yaitu f:A→B yang bersifat injektif dan surjektif sekaligus.
B.Fungsi Komposisi:
Fungsi komposisi adalah menggabungkan dua buah fungsi seperti f(x) dan g(x) yang akan menghasilkan sebuah fungsi baru dengan menggunakan sistem operasi komposisi.Dimana operasi komposisi biasa dilambangkan dengan "o"(komposisi/bundaran),dimana fungsi baru yang dapat di bentuk dari f(x) dan g(x) yaitu:
(f o g)(x) artinya g dimasukkan ke f
(g o f)(x) artinya f dimasukkan ke g
kemudian fungsi komposisi dapat ditulis sebagai berikut :
Sifat-sifat Fungsi Komposisi
1. Berlaku sifat asosiatif,contohnya:(f o(g o h))(x) = ((f o g)o h)(x).
2. Tidak berlaku sifat komutatif,contohnya: (f o g)(x) ≠ (g o f)(x).
3. Terdapat unsur identitas (I)(x),(f o I)(x) = (I o f)(x) = f(x).
Contoh soal dan penyelesaiannya:
Dik:f(x)=3x-2, g(x)=x²+1
1.Tentukan (f o g)(x).
2.Tentukan (g o f)(x).
jawab:
1.(f o g)(x) = f(g(x)) = f(x²+1) = 3(x2+1)-2 = 3x²+3-2 = 3x²+1
2.(g o f)(x) = g(f(x)) = g(3x-2) =(3x-2)²+1 =9x²-12x+4+1=9x²-12x+5
C.Fungsi Invers
yaitu fungsi dari himpunan A ke B dinyatakan dengan f,sehingga invers dari fungsi f merupakan relasi dari himpunan A ke B.maka untuk fungsi invers dari f:A→B adalah f-1:B→A. Sehingga kesimpulannya yaitu daerah hasil dari f-1(x) adalah daerah asal untuk f(x) dan sebaliknya, contohnya: jika y = f(x) maka x = f-1(y).
Cara untuk menentukan fungsi invers,yaitu bila fungsi f(x) telah diketahui :
Langkah 1:
Ubah persamaan y=f(x) menjadi bentuk x sebagai fungsi dari y
Langkah 2:
hasil dari perubahan bentuk x sebagai fungsi y itu dinamakan sebagai f-1(y)
Langkah 3:
Ubah y menjadi x [f-1(y) menjadi f-1(x)].
Contoh soal dan pembahasan:
Tentukan fungsi invers dari persamaan berikut
Untuk materi lain klik gambar di bawah ini:
Untuk materi sebelumnya klik gambar di bawah ini:
Untuk materi selanjutnya
Cukup sekian untuk pembahasan kali ini,silahkan jika ingin berkomentar atau memberikan saran,mohon maaf apabila ada kesalahan semoga pembahasan ini dapat bermanfaat.Dalam pembuatan artikel ini tak luput dari referensi yaitu dari beberapa situs, jika artikel di atas terdapat kekeliruan atau kesalahan,mohon untuk hubungi saya melalui contact atau melalui komentar.
Referensi:
http://www.utakatikotak.com/kongkow/detail/1662/-Fungsi-Komposisi-dan-Invers
http://www.rumusmatematikadasar.com/2015/01/pembahasan-fungsi-komposisi-dan-fungsi-invers.html
https://www.wardayacollege.com/matematika/aljabar/fungsi-komposisi-fungsi-invers/
https://rumushitung.com/2013/11/02/fungsi-komposisi-fungsi-dan-invers-fungsi-matematika/
https://tanya-tanya.com/rangkuman-contoh-soal-pembahasan-fungsi-komposisi/
https://ngestipramda.wordpress.com/2014/03/25/fungsi-komposisi-fungsi-dan-invers-fungsi-matematika/
https://id.wikipedia.org
https://dwideasy.wordpress.com/2014/05/18/pengertian-fungsi-dalam-matematika/
https://easymathuls.wordpress.com/2017/05/18/fungsi-surjektif-injektif-bijektif/
https://id.wikipedia.org/wiki/Daftar_simbol_matematika
http://naturalsaints.blogspot.com/2009/05/bilangan-pangkat-negatif.html
Fungsi adalah pemetaan dari setiap anggota dimana menghubungkan setiap anggota A dalam suatu himpunan yang dinamakan domain(daerah asal) kepada anggota himpunan lain dengan tepat satu anggota himpunan B atau juga dengan suatu nilai tunggal f(x) dari himpunan yang kedua yang di sebut kodomain(daerah kawan),kemudian himpunan nilai dari hasil tersebut disebut dengan range (daerah hasil).
Keterangan:
- Himpunan A adalah domain (daerah asal)
- Himpunan B adalah kodomain (daerah kawan)
- Himpunan anggota B yaitu C (f(x)) adalah range (hasil)
Sifat-sifat Fungsi :
1).Fungsi Injektif(satu-satu)
Dimana fungsi injektif(satu-satu),hanya mempunyai satu kawan saja,misalnya fungsi
f menyatakan A ke B atau f:A→B,dimana setiap anggota di dalam B hanya memiliki satu kawan saja di A,sehingga fungsi injektif apabila a ≠ b berakibat f(a) ≠ f(b) atau ekuivalen, jika f(a) = f(b) maka akibatnya a = b,untuk contohnya bisa di lihat gambar di bawah ini:
fungsi surjektif dimana setiap elemen himpunan B yaitu merupakan bayangan dari satu atau lebih elemen himpunan A,atau pada fungsi f:A→B,dimana setiap b∈B mempunyai kawan di A.
3).Fungsi Bijektif (Korespondensi satu-satu)
yaitu f:A→B yang bersifat injektif dan surjektif sekaligus.
B.Fungsi Komposisi:
Fungsi komposisi adalah menggabungkan dua buah fungsi seperti f(x) dan g(x) yang akan menghasilkan sebuah fungsi baru dengan menggunakan sistem operasi komposisi.Dimana operasi komposisi biasa dilambangkan dengan "o"(komposisi/bundaran),dimana fungsi baru yang dapat di bentuk dari f(x) dan g(x) yaitu:
(f o g)(x) artinya g dimasukkan ke f
(g o f)(x) artinya f dimasukkan ke g
kemudian fungsi komposisi dapat ditulis sebagai berikut :
- Untuk (f o g)(x)=f(g(x))→ komposisi g(yaitu fungsi f bundaran g atau juga fungsi komposisi dengan g dikerjakan lebih dahulu daripada f)
- Untuk (g o f)(x)=g(f(x))→ komposisi f(yaitu fungsi g bundaran f atau juga fungsi komposisi dengan f dikerjakan lebih dahulu daripada g)
Sifat-sifat Fungsi Komposisi
1. Berlaku sifat asosiatif,contohnya:(f o(g o h))(x) = ((f o g)o h)(x).
2. Tidak berlaku sifat komutatif,contohnya: (f o g)(x) ≠ (g o f)(x).
3. Terdapat unsur identitas (I)(x),(f o I)(x) = (I o f)(x) = f(x).
Contoh soal dan penyelesaiannya:
Dik:f(x)=3x-2, g(x)=x²+1
1.Tentukan (f o g)(x).
2.Tentukan (g o f)(x).
jawab:
1.(f o g)(x) = f(g(x)) = f(x²+1) = 3(x2+1)-2 = 3x²+3-2 = 3x²+1
2.(g o f)(x) = g(f(x)) = g(3x-2) =(3x-2)²+1 =9x²-12x+4+1=9x²-12x+5
C.Fungsi Invers
yaitu fungsi dari himpunan A ke B dinyatakan dengan f,sehingga invers dari fungsi f merupakan relasi dari himpunan A ke B.maka untuk fungsi invers dari f:A→B adalah f-1:B→A. Sehingga kesimpulannya yaitu daerah hasil dari f-1(x) adalah daerah asal untuk f(x) dan sebaliknya, contohnya: jika y = f(x) maka x = f-1(y).
Cara untuk menentukan fungsi invers,yaitu bila fungsi f(x) telah diketahui :
Langkah 1:
Ubah persamaan y=f(x) menjadi bentuk x sebagai fungsi dari y
Langkah 2:
hasil dari perubahan bentuk x sebagai fungsi y itu dinamakan sebagai f-1(y)
Langkah 3:
Ubah y menjadi x [f-1(y) menjadi f-1(x)].
Contoh soal dan pembahasan:
Tentukan fungsi invers dari persamaan berikut
Untuk materi lain klik gambar di bawah ini:
Untuk materi sebelumnya klik gambar di bawah ini:
Untuk materi selanjutnya
Cukup sekian untuk pembahasan kali ini,silahkan jika ingin berkomentar atau memberikan saran,mohon maaf apabila ada kesalahan semoga pembahasan ini dapat bermanfaat.Dalam pembuatan artikel ini tak luput dari referensi yaitu dari beberapa situs, jika artikel di atas terdapat kekeliruan atau kesalahan,mohon untuk hubungi saya melalui contact atau melalui komentar.
Referensi:
http://www.utakatikotak.com/kongkow/detail/1662/-Fungsi-Komposisi-dan-Invers
http://www.rumusmatematikadasar.com/2015/01/pembahasan-fungsi-komposisi-dan-fungsi-invers.html
https://www.wardayacollege.com/matematika/aljabar/fungsi-komposisi-fungsi-invers/
https://rumushitung.com/2013/11/02/fungsi-komposisi-fungsi-dan-invers-fungsi-matematika/
https://tanya-tanya.com/rangkuman-contoh-soal-pembahasan-fungsi-komposisi/
https://ngestipramda.wordpress.com/2014/03/25/fungsi-komposisi-fungsi-dan-invers-fungsi-matematika/
https://id.wikipedia.org
https://dwideasy.wordpress.com/2014/05/18/pengertian-fungsi-dalam-matematika/
https://easymathuls.wordpress.com/2017/05/18/fungsi-surjektif-injektif-bijektif/
https://id.wikipedia.org/wiki/Daftar_simbol_matematika
http://naturalsaints.blogspot.com/2009/05/bilangan-pangkat-negatif.html















EmoticonEmoticon